|     © 2019   |      AE911Truth.CH

Die Zerstörung des Nordturms des World Trade Centers

und die Fundamentalphysik

von David Chandler

(Übersetzung von Andreas Bertram-Weiss)

Teil 2

4.  Beobachtungen

Für diese Analyse folgen wir Bazănts vereinfachenden Annahmen [4, 5, 6, 7], indem wir den oberen Teil des Gebäudes als einen festen Block mit der Masse m betrachten. Die einzigen zwei relevanten Kräfte, welche auf den fallenden Block wirken, sind die Schwer- bzw. Gravitätskraft (mg) und eine aufwärts gerichtete Normalkraft (N), welche aufgrund ihrer Wechselwirkung mit dem unteren Teil des Gebäudes auftritt.

Gemäss Newtons Zweitem Gesetz erhalten wir, wenn die Gleichung nach N aufgelöst wird:

mg  - N =  ma

N =  mg  - ma     (3)

Unsere Messung zeigt an, dass ab dem 6. errechneten Geschwindigkeitsmesspunkt an der obere Block sich gleichförmig beschleunigt (R2-Wert von 0.997) mit

a = - 6.31 m/s2, oder in anderen Worten,

mit 64% der Beschleunigung des Freien Falls.  Für diesen Wert von a ist  

N =  mg - 0.64 mg = 0.36 mg   . (4)

So liegt die aufwärts gerichtete Normalkraft bei 36% des Gewichts des oberen Blocks, wie es in Bild 3 dargestellt ist.

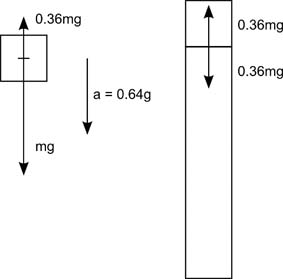
Bild 3:  Nehmen wir an, dass der obere Teil des Gebäudes ein Block mit dem Gewicht mg ist. Da die Beschleunigung des Blocks gemessen wird mit 0.64g abwärts, muss die resultierende Kraft, welche auf ihn wirkt, 0.64mg sein.

Die Schwerkraft ist mg, so muss die aufwärts gerichtete Normalkraft 0.36mg sein. Der obere und der untere Teil des Gebäudes üben gleiche aber entgegensetzte Kräfte aufeinander aus, so dass das Gewicht, welches auf den unteren Teil des Gebäudes wirkt, 36% des Gewichts des oberen Blocks beträgt.

 

Ausdrücklich sei Newtons Drittes Gesetz hier angeführt, welches das Ergebnis in ein anderes Licht rückt.

Da die Kräfte in dieser Interaktion gleich und gegengesetzt wirken, übt der fallende Block eine Kraft von nur 36% seines Gewichts auf den unteren Teil des Gebäudes aus.

In anderen Worten, solange der fallende Block sich weiter abwärts beschleunigt, haben wir ein Ergebnis, welches dem intuitiven Wissen widerspricht, dass nämlich die Kraft, die er auf den unteren Teil des Gebäudes ausübt, bedeutend geringer als sein statisches Gewicht ist.

Es ist schwierig sich vorzustellen, wie ein oberer Block, welcher eine Kraft von nur 36% seines statischen Gewichts ausübt, einen grösseren, solideren und unbeschädigten unteren Gebäudeteil bis zum Erdboden zerschlagen kann, obwohl das Gebäude auf jeder Höhe so konstruiert war, um ein Mehrfaches des Gewichts über ihm zu tragen.

Wenn man einen Sicherheitsfaktor zwischen 3 und 5 annimmt [12], dann bedeutet die beobachtete Beschleunigung, dass etwa bis zu 90% der Festigkeit des unteren Teils des Gebäudes von Kräften beseitigt worden sind, welche andere sein müssen als der angenommene "Rammhammer", was ein Hinweis darauf ist, dass dabei eine Art geplanter Sprengung verwendet wurde.

Man kann hinsichtlich der Festigkeit der verschiedenen Bauelemente argumentieren, dass der Aufschlag des fallenden Blocks den unteren Teil des Gebäudes wohl zerschlagen könnte (obwohl diese Behauptung bestritten wurde [13]), aber es kann nicht zugleich den unteren Block zermalmen, während es gleichzeitig die abwärts gerichtete Beschleunigung beibehält.

Prof. Graeme MacQueen und Tony Szamboti machten parallel die Beobachtung, welche auf einer ähnlichen Messung beruht, in ihrem Aufsatz "The Missing Jolt: A Simple Refutation of the NIST--Bazănt Collapse Hypothesis."(Der fehlende Ruck: eine einfache Widerlegung der Einsturzhypothese von NIST-Bazănt). [14]

Sie zeigen darin auf, dass eine zunehmende Kraft auf den unteren Teil des Gebäudes von einer Abnahme des Impulses des fallenden Block begleitet sein muss. Die Übertragung des Impulses (welcher einen Verlust von Impulskraft für den oberen Block bedeutet) ist es, was den Impuls hervorruft. Er sollte daher einen "Ruck" erfahren, welchen wir auch in der Videoanalyse sehen können sollten. Aber aus der Tatsache, dass der obere Block sich ohne Verzögerung kontinuierlich nach unten bewegt, wird deutlich, dass es keinen Ruck gab, ungeachtet der erheblichen Verformung des Gebäudes in den ersten drei Sekunden.

Die Tatsache, dass ein sich abwärts beschleunigender Block eine Kraft auf den Zielblock ausüben würde, die kleiner ist als sein eigenes Gewicht, ist intuitiv schwierig zu begreifen, weil unsere Erfahrung uns nahelegt, dass der untere Zielblock dem zermalmenden Schlag widerstehen würde. Ein schnell bewegter Hammerkopf, welcher einen Nagel in einen massiven Holzblock treibt, übt normalerweise eine Kraft auf den Nagel aus, welche viele Male höher ist als das Gewicht des Hammerkopfes. Aber dies ist nur wahr, wenn der Nagel dem Schlag widersteht. Der starken Kraft, die den Nagel in das Holz treibt, wird von einer (Gegen-)Kraft entsprochen, die gleichzeitig den Hammerkopf abbremst, weshalb normalerweise mehrere Schläge benötigt werden. Wenn jedoch der Nagel auf einem Block Styroporschaum platziert wird, dann wird er nicht besonders dem Schlag entgegenwirken. Er würde durch eine sehr kleine Kraft in den Block gehauen. Der fallende Hammerkopf würde so eine kleine Widerstandskraft erfahren, dass er in der Lage wäre, die ganze Zeit zu beschleunigen.

Im Fall von WTC 1 agiert der fallende Block wie ein Hammerkopf, der in Styropor gehauen wird. Aber, um das Bild etwas zu verändern, es ist die Verbindung zwischen den zwei Blöcken, welche "weich" ist. Etwas anderes als der fallende Block muss die bauliche Stabilität der Grenzflächenzone zerstören (wie etwa Sprengstoffe ?), so dass diese nur noch einen kleinen Teil des Widerstandes bietet, der einmal dazu entworfen wurde, dass er Halt bietet.

Einige mögen entgegnen, dass dieses Modell doch etwas zu sehr vereinfacht.

Es wurde als Argument angeführt, dass das zermalmte Material an der Verbindungsstelle der Zerstörung zu dem oberen Teil hinzugefügt wird, so dass die Masse des fallenden Blocks anwächst, während er fällt, wobei er einen Lawineneffekt hervorruft. [15]

Ich würde von der Tatsache her argumentieren, dass ein grösserer Teil der Masse ausserhalb des Grundrisses des Gebäudes landete, diese Zunahme allenfalls anteilig gewesen war. Aber lassen Sie uns die Auswirkung einer solchen Zunahme bedenken.

Newtons Zweites Gesetz angewendet auf ein System von variablen Massen kann angeführt werden mit

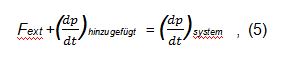
wobei p der Impuls ist und  Fext  stellt die resultierende äussere Kraft dar, welche auf das System wirkt.  Die hinzugefügte Masse ist anfangs in Ruhe, so bringt sie keinen neuen Impuls in das System:

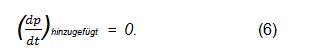
Da   p = mv ist, können wir schreiben,

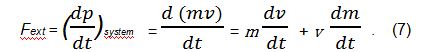
In unserer Situation (lassen wir die Richtung abwärts positiv sein),

Fext  =  mg - N                    (8)

wobei N die Normalkraft ist, wie in unserer vorherigen Analyse.

Wir erkennen in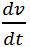                          

 einfach die Beschleunigung a, so können wir schreiben

(mg - N) = ma + v 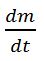  .     (9)

Nach N auflösend, erhalten wir

N = mg - ma - v 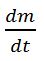      .     (10)

Bemerken Sie bitte, dass dies das gleiche Ergebnis ist wie das vorausgehende (Gleichung  3), ausser dass die Normalkraft weiter reduziert wurde, da

sowohl v wie auch 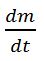     positiv sind.

Deshalb reduziert, vielleicht gegen unsere Intuition, jedes hinzugefügte Material den Wirkungsgrad eines angenommenen Rammhammers.

Dieses Ergebnis kann aber ziemlich anschaulich werden, wenn man erkennt, dass der fallende Block von seinem Impuls etwas auf die hinzugefügte Masse übertragen muss, um diese auf seine Geschwindigkeit zu bringen .

5. Zusammenfassung

Die Tatsache, dass die Dachlinie des oberen Teils des Nordturm sich kontinuierlich abwärts beschleunigte, auch durch die Kollision mit dem unteren Teil des Gebäudes hindurch, weist darauf hin, dass der obere Teil nicht wie ein Rammgerät wirken konnte. Solange die Dachlinie sich nach unten beschleunigte, übte der obere Block eine Kraft auf den unteren Teil des Gebäudes aus, welche geringer war als sein eigenes statisches Gewicht.

Jegliches Zunahme von Material zu dem oberen Block hätte als eine träge Bremse gewirkt, welche die Kraft der Interaktion nur noch weiter reduziert hätte.

Der unbeschädigte untere Teil des Gebäudes wurde so gebaut, dass er ein Mehrfaches des Gewichts von dem Material über ihm trägt, aber ob wir nun den Sicherheitsfaktor mit einbeziehen oder nicht, die reduzierte Kraft, welche durch die fallende Masse ausgeübt wurde, konnte nicht das sein, was die gewaltsame Zerstörung des Gebäudes verursachte, wie es in zahlreichen Videos zu sehen ist.

Die andauernde Beschleunigung des oberen Teils des Gebäudes ist vielmehr eine überzeugende Bestätigung dafür, dass eine andere Energiequelle verwendet wurde, um die Baustruktur unterhalb von dieser zu entfernen. Dies ermöglichte es dem oberen Teil, mit nur einem geringen Widerstand zu fallen.

Mit der Annahme, dass es einen unzerstörten fallenden Block gab, mit oder ohne Zunahme von Material, haben wir angesichts der beobachteten Beschleunigung gezeigt, dass ein solcher Block nicht  den unteren Teil des Gebäudes zerstört haben konnte.

Wenn wir uns dem Videobeweis zuwenden, dann sehen wir, dass selbst eine hypothetische Existenz eines überdauernden oberen Block eine Fiktion ist.

Die Videos zeigen, dass der Teil des Gebäudes oberhalb der Stelle des Flugzeugeinschlags gerade der erste Teil war, der sich auflöste. Er wurde massgeblich in der Grösse reduziert, bevor die Zerstörung des unteren Teils des Gebäudes einsetzte. Sobald die Dachlinie in die Schuttwolke hinabsinkt, gibt es keinen Hinweis für ihre weiter bestehende Existenz. Ob sie nun so früh bei dem Einsturz völlig zerstört wurde oder nicht, ist ein irrelevanter Punkt.

Wir haben gezeigt, dass sie sogar, wenn sie intakt weiter fortbestand, keine bedeutende Rolle in der Zerstörung des Gebäudes gespielt haben konnte.

Ein kleiner Teil einer Baustruktur, welcher aus wenigen Stockwerken besteht, kann nicht in eine Richtung einen bedeutend grösseren unteren Teil mit der gleichen Baustruktur allein aufgrund von Schwerkraft niederdrücken.

6. Danksagung

Ich möchte meine Wertschätzung dem Team der Freiwilligen von Architects & Engineers for 9/11 Truth und anderen in der weiteren Gemeinschaft, die sich für die Wahrheit vom 11. September einsetzen, ausdrücken, welche mit Ermutigung und kritischer Diskussion zu diesem Aufsatz beitrugen. Auch würdige ich den Austausch mit Charles M. Beck, welcher mich dazu brachte, über die Bedeutung der Massenzunahme für diese Analyse nachzudenken.

Diesen Aufsatz finden Sie auch hier als pdf zum Download …

7.  Anmerkungen und Verweise

[4] Z. P. Bazănt, “Why did the World Trade Center collapse?” SIAM News, vol. 34, no. 8, pp. 2-6, 2001, (Es ist bemerkenswert, dass dieser Aufsatz am 13. September veröffentlicht wurde, d.h. zwei Tage nach 9/11).

[Online]. Available: http://www-math.mit.edu/~bazant/WTC/ [Accessed Mar 1, 2009]

[5] Z. P. Bazănt and Y. Zhou, “Why did the World Trade Center collapse—Simple analysis,” J. Eng. Mech., vol. 128, no. 1, pp. 2-6, 2002.[Online]. Available: http://www-math.mit.edu/~bazant/WTC/WTC-asce.pdf [Accessed Mar1, 2009]

[6] Z. P. Bazănt and M. Verdure, “Mechanics of progressive collapse: Learning from World Trade Center and building demolitions,” J. Eng. Mech., vol. 133, no. 3, pp. 308-319, 2007. [Online].

Available: http://www.civil.northwestern.edu/people/bazant/PDFs/Papers/466.pdf [Accessed Mar 1, Journal of 9/11 Studies - Feb 2010 16 2009]

[7] Bazănt, Le, Greening and Benson, Journal of Engineering Mechanics, ASCE, Vol. 134 (2008), “

What Did and Did not Cause Collapse of WTC Twin Towers in New York” Available: http://wtc7lies.googlepages.com/Bazant_WTC_Collapse_What_Did__Did_No.pdf

[12] T. Szamboti. (2007, May) The sustainability of the controlled demolition hypothesis for the destruction of the Twin Towers. [Online]. Available: http://www.journalof911studies.com/ [Accessed Mar 1, 2009]

[13] G. Ross. (2006, Jun.) Momentum transfer analysis of the collapse of the upper storeys of WTC 1. [Online]. Available: http://www.journalof911studies.com/articles/Journal_5_PTransferRoss.pdf [Accessed Mar 1, 2009]

[14] G. MacQueen and T. Szamboti. (2009, Jan.) The missing jolt: A simple refutation of the NISTBaz_nt collapse hypothesis. [Online]. Available: http://www.journalof911studies.com/volume/2008/TheMissingJolt7.pdf [Accessed Mar 1, 2009]

[15] C. M. Beck. (2007, Nov.) Mathematical models of progressive collapse and the question of how did the World Trade Centers perish. [Online]. Available: http://arxiv.org/PS_cache/physics/pdf/0609/0609105v8.pdf [Accessed Mar 1, 2009]